Câu hỏi:
03/04/2024 39\(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 5x + 1}}{{1 + 3x - {x^2}}}\) bằng:
A. +¥
B. 2
C. −2
D. 1
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 5x + 1}}{{1 + 3x - {x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {2 - \frac{5}{x} + \frac{1}{{{x^2}}}} \right)}}{{{x^2}\left( {\frac{1}{{{x^2}}} - \frac{3}{x} - 1} \right)}} = - 2.\)
Hướng dẫn giải
Đáp án đúng là: C
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 5x + 1}}{{1 + 3x - {x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}\left( {2 - \frac{5}{x} + \frac{1}{{{x^2}}}} \right)}}{{{x^2}\left( {\frac{1}{{{x^2}}} - \frac{3}{x} - 1} \right)}} = - 2.\)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x) = \(\frac{1}{3}\)x3 + 2x2 – \(\frac{2}{3}\) có đồ thị (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến song song với đường thẳng d: y = −4x + 2022.
Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC) và SA = a. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và có SA = SC, SB = SD. Trong các khẳng định sau, khẳng định nào đúng?
Câu 4:
Đường thẳng y = ax + b tiếp xúc với đồ thị hàm số y = x3 – 3x – 1 tại điểm có hoành độ bằng 2, giá trị của a + b bằng:
Câu 5:
Phương trình tiếp tuyến của đồ thị hàm số y = x4 – 3x2 + 1 tại điểm M(1;−1) là:
Câu 7:
Gọi H là hình chiếu vuông góc của A trên SC. Chứng minh AH ^ BD và tính độ dài đoạn AH.
Câu 9:
Cho chuyển động thẳng xác định bởi phương trình S = 2t4 – 9t2 + 3, trong đó t được tính bằng giây và S được tính bằng mét. Vận tốc của chuyển động tại thời điểm t = 2 (giây) là:
Câu 11:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Trong các khẳng định sau, khẳng định nào sai?
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với cạnh AB = \(a\sqrt 2 \), SA vuông góc với mặt phẳng đáy và SA = 3a.
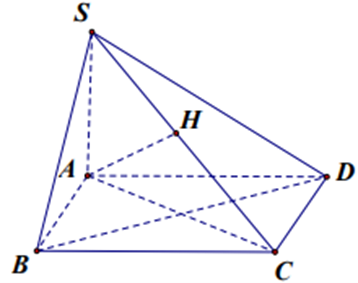
Chứng minh CD ^ (SAD).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với cạnh AB = \(a\sqrt 2 \), SA vuông góc với mặt phẳng đáy và SA = 3a.

Chứng minh CD ^ (SAD).
Câu 13:
\(\mathop {\lim }\limits_{x \to {{( - 2)}^ - }} \frac{{5 - 3x}}{{x + 2}}\) bằng:
Câu 14:
Giải bất phương trình f'(x) > −1, biết rằng f(x) = (x2 – 2x)(x – 3).
Câu 15:
\(\mathop {\lim }\limits_{x \to 2} \left( { - 3{x^2} + 6x + 1} \right)\) bằng:


