Kí hiệu SABC là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC

Bài 9.35 trang 83 Toán 7 Tập 2:

Kí hiệu S_ABC là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC.

a) Chứng minh S_GBC = $\frac{1}{3}$S_ABC.

Gợi ý. Sử dụng GM = $\frac{1}{3}$AM để chứng minh S_GBM = $\frac{1}{3}$S_ABM, S_GCM = $\frac{1}{3}$S_ACM.

b) Chứng minh S_GCA = S_GAB = $\frac{1}{3}$S_ABC.

Nhận xét. Từ bài tập trên ta có: S_GBC = S_GCA = S_GAB = $\frac{1}{3}$S_ABC, điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó.

Trả lời

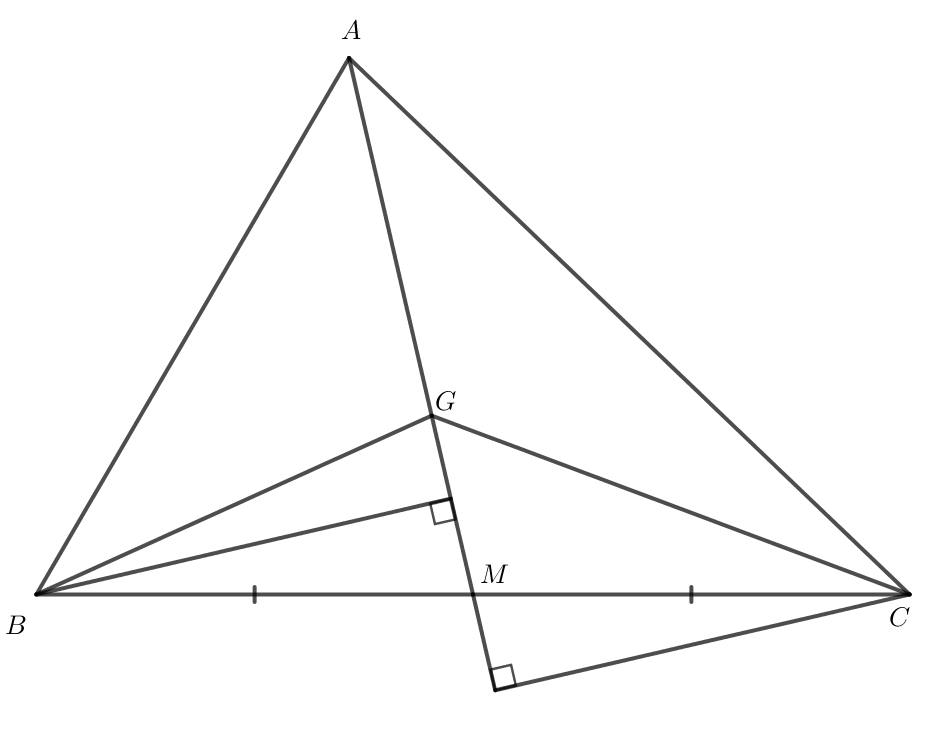a) Do G là trọng tâm của tam giác ABC và M là trung điểm của BC nên GM = $\frac{1}{3}$AM.

$∆$ABM và $∆$MBG có chung đường cao kẻ từ B đến AM nên tỉ số diện tích giữa MBG và $∆$ABM bằng tỉ số của hai đáy GM và AM.

Ta có GM = $\frac{1}{3}$AM nên S_MBG = $\frac{1}{3}$S_ABM.

$∆$ACM và $∆$MCG có chung đường cao kẻ từ C đến AM nên tỉ số diện tích giữa $∆$MCG và $∆$ACM bằng tỉ số của hai đáy GM và AM.

Ta có GM = $\frac{1}{3}$AM nên S_MCG = $\frac{1}{3}$S_ACM.

Do đó S_MBG + S_MCG = $\frac{1}{3}$S_ABM + $\frac{1}{3}$S_ACM

Hay S_GBC = $\frac{1}{3}$(S_ABM + S_ACM) = $\frac{1}{3}$S_ABC.

b) Chứng minh tương tự câu a:

Do G là trọng tâm của $∆$ABC nên AG = 2GM suy ra S_GCA = 2S_MCG; S_GAB = 2S_MBG.

Do BC = 2MB = 2MC nên S_GBC = 2S_MCG = 2S_MBG.

Do đó S_GCA = S_GAB = S_GBC = $\frac{1}{3}$S_ABC.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 33: Quan hệ giữa ba cạnh của một tam giác

Luyện tập chung trang 71

Bài 34: Sự đồng quy của ba đường trung tuyến. Ba đường phân giác trong một tam giác

Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Luyện tập chung trang 83

Bài tập cuối chương 9