Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?
Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?
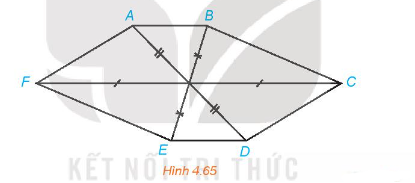
Lời giải:
+) Xét hình lục giác đều MNPQRS có tâm O.
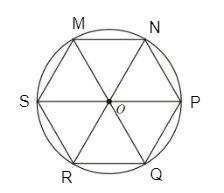
Ta nhận thấy:
- Tứ giác OSMN là hình thoi;
- Các điểm P, Q, R lần lượt là các điểm đối xứng của các điểm S, M, N qua tâm O.
Từ đó suy ra các vẽ hình biểu diễn của hình lục giác đều MNPQRS như sau:
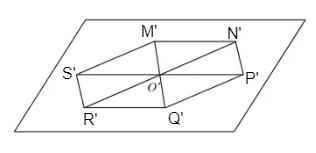
- Vẽ hình bình hành O'S'M'N' biểu diễn cho hình thoi OSMN;
- Lấy các điểm P', Q', R' lần lượt là các điểm đối xứng của các điểm S', M', N' qua O', ta được hình biểu diễn M'N'P'Q'R'S' của hình lục giác đều MNPQRS.
+) Gọi I là giao điểm các đường chéo AD, BE và CF trong hình lục giác ABCDEF ở Hình 4.65.
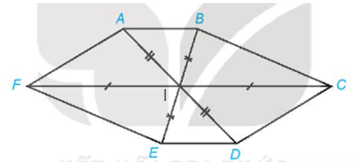
Khi đó nếu ABCDEF là hình biểu diễn của hình lục giác đều thì phải thỏa mãn hai điều kiện:
- Tứ giác IFAB là hình bình hành (1);
- D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua I (2).
Từ hình vẽ ta thấy điều kiện (2) thỏa mãn nhưng điều kiện (1) không thỏa mãn. Vậy Hình 4.65 không thể là hình biểu diễn của một hình lục giác đều.