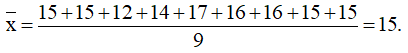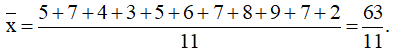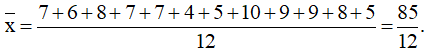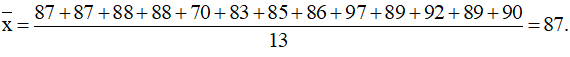Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau: a) 15; 15; 12; 14; 17; 16; 16; 15; 15

Bài 1 trang 122 SBT Toán 10 Tập 1: Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a) 15; 15; 12; 14; 17; 16; 16; 15; 15.

b) 5; 7; 4; 3; 5; 6; 7; 8; 9; 7; 2.

c) 7; 6; 8; 7; 7; 4; 5; 10; 9; 9; 8; 5.

d) 87; 87; 88; 88; 70; 83; 85; 86; 97; 89; 92; 89; 90.

Trả lời

a) Ta có: n = 9

Sắp xếp mẫu số liệu theo thứ tự không giảm:

12; 14; 15; 15; 15; 15; 16; 16; 17

+) Số trung bình:

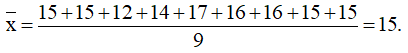
+) Vì n = 9 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 15.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 12; 14; 15; 15.

Vậy Q₁ = (14 + 15) : 2 = 14,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 15; 16; 16; 17.

Vậy Q₃ = (16 + 16) : 2 = 16.

+) Vì số 15 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (4 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 15.

b) Ta có: n = 11

Sắp xếp mẫu số liệu theo thứ tự không giảm:

2; 3; 4; 5; 5; 6; 7; 7; 7; 8; 9

+) Số trung bình:

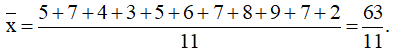
+) Vì n = 11 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 6.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 2; 3; 4; 5; 5.

Vậy Q₁ = 4.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 7; 7; 7; 8; 9.

Vậy Q₃ = 7.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

c) Ta có: n = 12

Sắp xếp mẫu số liệu theo thứ tự không giảm:

4; 5; 5; 6; 7; 7; 7; 8; 8; 9; 9; 10

+) Số trung bình:

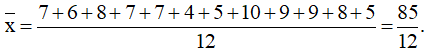
+) Vì n = 12 là số chẵn nên ta có tứ phân vị thứ hai Q₂ = (7 + 7) : 2 = 7.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, gồm Q₂ vì n là số chẵn: 4; 5; 5; 6; 7; 7.

Vậy Q₁ = (5 + 6) : 2 = 5,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, gồm Q₂ vì n là số chẵn: 7; 8; 8; 9; 9; 10.

Vậy Q₃ = (8 + 9) : 2 = 8,5.

+) Vì số 7 là giá trị xuất hiện nhiều nhất trong mẫu số liệu (3 lần). Nên suy ra Mốt của mẫu số liệu là M_o = 7.

d) Ta có: n = 13

Sắp xếp mẫu số liệu theo thứ tự không giảm:

70; 83; 85; 86; 87; 87; 88; 88; 89; 89; 90; 92; 97

+) Số trung bình:

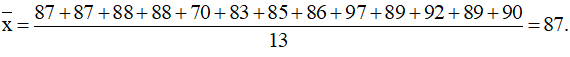
+) Vì n = 13 là số lẻ nên ta có tứ phân vị thứ hai Q₂ = 88.

Tứ phân vị thứ nhất là trung vị của nửa số liệu bên trái Q₂, không kể Q₂ vì n là số lẻ: 70; 83; 85; 86; 87; 87.

Vậy Q₁ = (85 + 86) : 2 = 85,5.

Tứ phân vị thứ ba là trung vị của nửa số liệu bên phải Q₂, không kể Q₂ vì n là số lẻ: 88; 89; 89; 90; 92; 97.

Vậy Q₃ = (89 + 90) : 2 = 89,5.

+) Vì số 87, 88, 89 là các giá trị xuất hiện nhiều nhất trong mẫu số liệu (2 lần). Nên suy ra Mốt của mẫu số liệu là M_o ∈ {87; 88; 89}.

Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Bài 4: Các số đặc trưng đo mức độ phân tán của mẫu số liệu

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai