Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y = ax + b, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh

Bài 7.29 trang 50 Toán 8 Tập 2: Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất y = ax + b, trong đó b biểu thị chi phí cố định của hoạt động kinh doanh và hệ số a biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 36 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là 1,8 triệu đồng.

a) Viết công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày.

b) Vẽ đồ thị hàm số thu được ở câu a.

c) Chi phí để sản xuất 15 chiếc xe đạp trong một ngày là bao nhiêu?

d) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngày, nếu chi phí trong ngày đó là 72 triệu đồng?

Trả lời

a) Chi phí cố định hằng ngày là 36 triệu đồng nên b = 36, chi phí sản xuất mỗi chiếc xe đạp là 1,8 triệu đồng nên a = 1,8.

Do đó, công thức của hàm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong một ngày là y = 1,8x + 36.

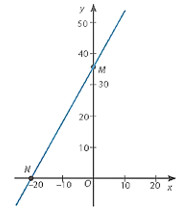
b) Cho x = 0 thì y = 36 ta được giao điểm của đồ thị hàm số với trục Oy là M(0; 36).

 Cho y = 0 thì x = –20, ta được giao điểm của đồ thị hàm số với trục Ox là N(–20; 0).

Đồ thị của hàm số y = 1,8x + 36 là đường thẳng MN.

c) Chi phí để sản xuất 15 chiếc xe đạp (tức x = 15) trong 1 ngày là: 

y = 1,8 . 15 + 36 = 63 (triệu đồng).

d) Thay y = 72 vào công thức hàm số y = 1,8x + 36 ta được:

72 = 1,8x + 36, suy ra x = 20 (chiếc xe).

Vậy với chi phí trong ngày là 72 triệu đồng thì có thể sản xuất được 20 chiếc xe đạp.

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung (trang 37)

Bài 27: Khái niệm hàm số và đồ thị của hàm số

Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất

Bài 29: Hệ số góc của đường thẳng

Luyện tập chung (trang 55)

Bài tập cuối chương 7