Câu hỏi:
03/04/2024 61
Giải bất phương trình f'(x) > −1, biết rằng f(x) = (x2 – 2x)(x – 3).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
f '(x) = (x2 – 2x)'. (x – 3) + (x – 3)'. (x2 – 2x)
= (2x – 2).(x – 3) + (x2 – 2x) = 3x2 – 10x + 6
f '(x) > −1 Û 3x2 – 10x + 6 > −1 Û 3x2 – 10x + 7 > 0
Tập nghiệm của bất phương trình là : S = (−¥;1) È (73;+∞).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x) = 13x3 + 2x2 – 23 có đồ thị (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến song song với đường thẳng d: y = −4x + 2022.
Câu 2:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC) và SA = a. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và có SA = SC, SB = SD. Trong các khẳng định sau, khẳng định nào đúng?
Câu 4:
Đường thẳng y = ax + b tiếp xúc với đồ thị hàm số y = x3 – 3x – 1 tại điểm có hoành độ bằng 2, giá trị của a + b bằng:
Câu 5:
Gọi H là hình chiếu vuông góc của A trên SC. Chứng minh AH ^ BD và tính độ dài đoạn AH.
Câu 6:
Phương trình tiếp tuyến của đồ thị hàm số y = x4 – 3x2 + 1 tại điểm M(1;−1) là:
Câu 8:
Cho hàm số f(x)={3-√4x+1x-2 . Hàm số đã cho liên tục tại x = 2 khi a bằng:
Câu 11:
Cho chuyển động thẳng xác định bởi phương trình S = 2t4 – 9t2 + 3, trong đó t được tính bằng giây và S được tính bằng mét. Vận tốc của chuyển động tại thời điểm t = 2 (giây) là:
Câu 12:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với cạnh AB = a\sqrt 2 , SA vuông góc với mặt phẳng đáy và SA = 3a.
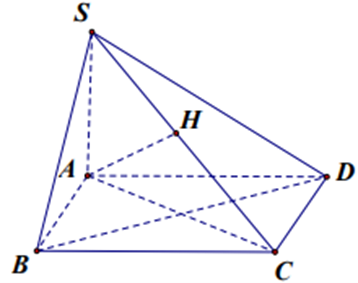
Chứng minh CD ^ (SAD).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông với cạnh AB = a\sqrt 2 , SA vuông góc với mặt phẳng đáy và SA = 3a.

Chứng minh CD ^ (SAD).
Câu 13:
Chứng minh rằng phương trình 2x4 – 3x3 – 5 = 0 có ít nhất một nghiệm.
Câu 14:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và có cạnh SA vuông góc với mặt phẳng (ABCD). Trong các khẳng định sau, khẳng định nào sai?


