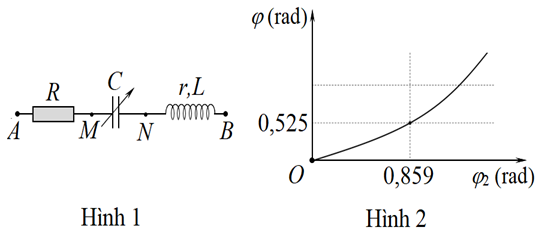
Đặt điện áp xoay chiều (có giá trị hiệu dụng và tần số không đổi) vào hai đầu đoạn mạch như hình 1 thì cảm kháng của cuộn dây \[{Z_L} = 3r.\] Gọi \[\varphi \] và \[{\varphi _2}\] tương ứng là độ lệch pha giữa điện áp \[{u_{AB}}\] và \[{u_{MB}}\] so với cường độ dòng điện trong đoạn mạch. Đồ thị biểu diễn sự phụ thuộc của \[\varphi \] vào \[{\varphi _2}\] khi điện dung thay đổi như hình 2. Khi \[C = {C_0}\] thì điện áp \[{u_{AN}}\] lệch pha \[{90^{\rm{o}}}\] so với \[{u_{MB}}.\] Khi đó hệ số công suất của đoạn mạch MB có thể nhận giá trị nào sau đây?

D. 0,46.

Chuẩn hóa \({Z_L} = 3r = 3\)

\(\left\{ \begin{array}{l}\tan {\varphi _2} = \frac{{{Z_L} - {Z_C}}}{r}\\\tan \varphi = \frac{{{Z_L} - {Z_C}}}{{R + r}}\end{array} \right. \Rightarrow \frac{{\tan {\varphi _2}}}{{\tan \varphi }} = \frac{{R + r}}{r} \Rightarrow \frac{{\tan 0,859}}{{\tan 0,525}} = \frac{{R + 1}}{1} \Rightarrow R \approx 1\)

Khi \({u_{AN}} \bot {u_{MB}} \Rightarrow \tan {\varphi _{AN}}\tan {\varphi _{MB}} = - 1 \Rightarrow \frac{{{Z_C}}}{R}.\frac{{{Z_L} - {Z_C}}}{r} = 1 \Rightarrow {Z_C}\left( {3 - {Z_C}} \right) = 1 \Rightarrow {Z_C} = \frac{{3 \pm \sqrt 5 }}{2}\)

\(\cos {\varphi _{MB}} = \frac{r}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{1}{{\sqrt {{1^2} + {{\left( {3 - \frac{{3 \pm \sqrt 5 }}{2}} \right)}^2}} }} \approx \left[ \begin{array}{l}0,93\\0,36\end{array} \right.\). Chọn B