Có bao nhiêu số nguyên $x\in [-2021;2021]$ để ứng với mỗi x có tối thiểu 64 số nguyên y thỏa mãn ${\log }_3\sqrt{x^4+y}\ge {\log }_2(x+y)$?

Ta có ${\log }_3\sqrt{x^4+y}\ge {\log }_2(x+y)\iff {\log }_9\left(x^4+y\right)\ge {\log }_2(x+y)\left(1\right)$

Đặt $t=x+y\in {\mathbb{N}}^{*}($ do $x,y\in \mathbb{Z},x+y>0$

${\text{g}}^{\text{'}}\left(\text{t}\right)=\frac{1}{\text{t}\ln 2}-\frac{1}{\left({\text{x}}^4-\text{x}+\text{t}\right)\ln 9}$ mà $\text{x}\in [-2021;2021]\Rightarrow {\text{x}}^4\ge \text{x}\Rightarrow {\text{x}}^4-\text{x}\ge 0\Rightarrow {\text{x}}^4-\text{x}+\text{t}\ge \text{t}$

Từ đó suy ra ${\text{g}}^{\text{'}}\left(\text{t}\right)=\frac{1}{\text{t}\ln 2}-\frac{1}{\left({\text{x}}^4-\text{x}+\text{t}\right)\ln 9}>0,\forall \text{x},\text{t}$ thuộc điều kiện xác định.

Do đó g(t) đồng biến trên $[1;+\infty )$

Mỗi một giá trị của x, y tương ứng với một giá trị của t nên để x nguyên có tối thiểu 64 giá trị $\text{t}\in {\mathbb{N}}^{*}$ ta có $\text{g}\left(64\right)\le 0\iff {\log }_{2}64-{\log }_9\left({\text{x}}^4-\text{x}+64\right)\le 0$

$\iff {\log }_9\left(x^4-x+64\right)\ge 6\iff x^4-x+64\ge 9^6\iff x^4-x-531377\ge 0(*)$

Đặt $f\left(x\right)=x^4-x-531377\Rightarrow f^{\text{'}}\left(x\right)=4x^3-1=0\iff x=\sqrt[3]{\frac{1}{4}}$, ta có bảng biến thiên như sau

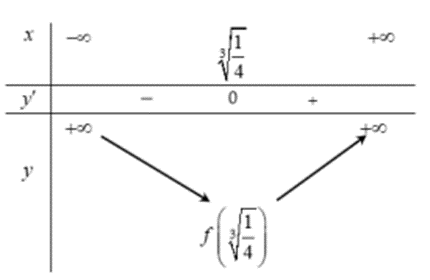
Lại có $\text{f}\left(26\right)=-74427;\text{f}\left(27\right)=37\Rightarrow \text{f}\left(26\right).\text{f}\left(27\right)<0$

$\text{f}(-26)=-74375;\text{f}(-27)=91\Rightarrow \text{f}(-26).\text{f}(-27)<0$

Do đó mỗi khoảng (26;27) và (-27;-26) phương trình f(x) = 0 có ít nhất một nghiệm.

Mà hàm số f(x) đồng biến trên mỗi khoảng $\left(-\infty ;\sqrt[3]{\frac{1}{4}}\right)$ và $\left(\sqrt[3]{\frac{1}{4}};+\infty \right)$ nên bất phương trình (*) có nghiệm $\left[\begin{array}{l}x\ge 27\\ x\le -27\end{array}\right.$. Kết hợp điều kiện $x\in [-2021;2021]$ và x nguyên suy ra

$x\in \{-2021;-2020;\dots ;-27;27;28;\dots ;2021\}$