Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình bình hành.
Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình bình hành.
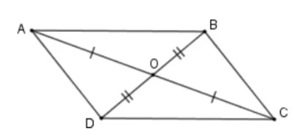
Gọi O là giao điểm của hai đường chéo.
Theo giả thiết ta có: OA = OC; OB = OD
Xét tam giác AOD và tam giác BOC có:
OA = OC
(đối đỉnh)
OB = OD
⇒ ∆AOD = ∆BOC (c.g.c)
Suy ra: AD = BC và
Mà ở vị trí so le trong nên AD // BC
Suy ra: ABCD là hình bình hành vì AD = BC và AD // BC.