Câu hỏi:
03/04/2024 54a) Chứng minh phương trình x5 + 4x3 - x2 - 1 = 0 có ít nhất một nghiệm thuộc khoảng (0; 1).
b) Tính limx→3√x−2−1x−3.
c) Xét tính liên tục của hàm số f(x)={x2+x−2x2−1 khi x<132x khi x≥1tại x = 1.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a) Xét hàm số f (x) = x5 + 4x3 - x2 - 1 là hàm liên tục
b) trên ℝ nên cũng liên tục trên khoảng (0; 1) (1)
Ta có: f(0) = –1; f(1) = 1 + 4 – 1 = 3
Do đó f (0).f (1) = (-1).3 = -3 < 0 (2)
Từ (1) và (2) suy ra phương trình f (x) = 0 cho ít nhất
một nghiệm x thuộc khoảng (0; 1).
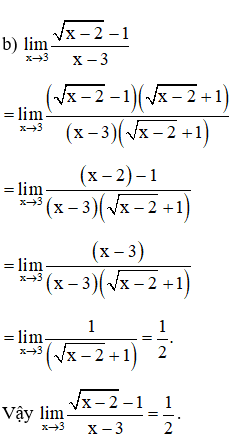
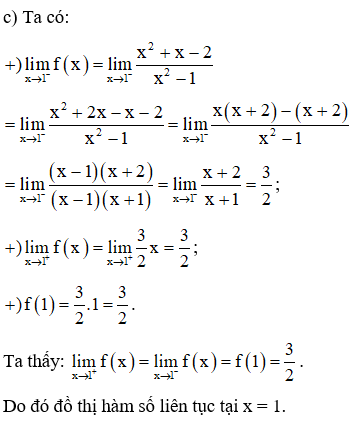
a) Xét hàm số f (x) = x5 + 4x3 - x2 - 1 là hàm liên tục
b) trên ℝ nên cũng liên tục trên khoảng (0; 1) (1)
Ta có: f(0) = –1; f(1) = 1 + 4 – 1 = 3
Do đó f (0).f (1) = (-1).3 = -3 < 0 (2)
Từ (1) và (2) suy ra phương trình f (x) = 0 cho ít nhất
một nghiệm x thuộc khoảng (0; 1).
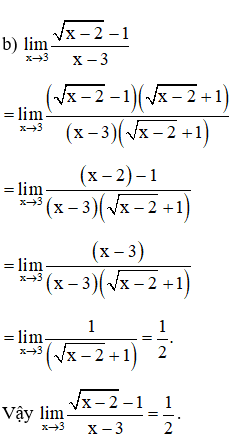
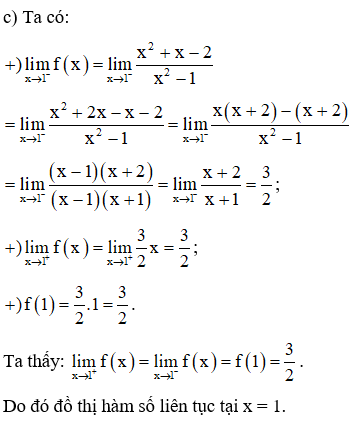
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hãy cho biết mệnh đề nào sau đây là sai? Hai đường thẳng vuông góc nếu:
Hãy cho biết mệnh đề nào sau đây là sai? Hai đường thẳng vuông góc nếu:
Xem đáp án »
03/04/2024
95
Câu 2:
Gọi φ là góc giữa 2 đường thẳng trong không gian. Chọn khẳng định đúng:
Xem đáp án »
03/04/2024
80
Câu 3:
Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính tích vô hướng →AB.→EG bằng:
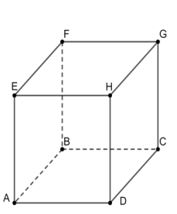

Xem đáp án »
03/04/2024
72
Câu 5:
Cho hình lập phương ABCD.A’B’C’D’. Hãy xác định góc giữa cặp vectơ →AB và →DD1 ?
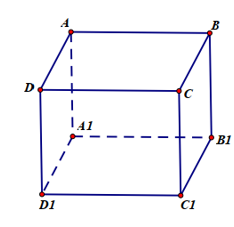
Cho hình lập phương ABCD.A’B’C’D’. Hãy xác định góc giữa cặp vectơ →AB và →DD1 ?

Xem đáp án »
03/04/2024
68
Câu 12:
Cho hình chóp S.ABCD có tất cả các cạnh bên đều bằng a và ASD = ASB.
a. Rút gọn P=→AB−→SB+→SD−→AC+→DC
b. Chứng minh rằng SA ^ BD
Cho hình chóp S.ABCD có tất cả các cạnh bên đều bằng a và ASD = ASB.
a. Rút gọn P=→AB−→SB+→SD−→AC+→DC
b. Chứng minh rằng SA ^ BD
Xem đáp án »
03/04/2024
62
Câu 13:
Cho hàm số f(x)={2x+1 khi x≠2a khi x=2 tìm a để hàm số liên tục tại x = 2.
Xem đáp án »
03/04/2024
61
Câu 14:
Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M0(x0; y0) là
Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M0(x0; y0) là
Xem đáp án »
03/04/2024
61