a) $4\cos x\cos \left(\frac{\pi }{3}-x\right)\cos \left(\frac{\pi }{3}+x\right)=\cos 3x;$

b) $\frac{\sin 2x\cos x}{\left(1+\cos x\right)\left(1+\cos 2x\right)}=\tan \frac{x}{2};$

c) sinx(1 + 2cos2x + 2cos4x + 2cos6x) = sin7x;

d) $\frac{{\sin }^{2}3x}{{\sin }^{2}x}-\frac{{\cos }^{2}3x}{{\text{cos}}^{2}x}=8\cos 2x.$

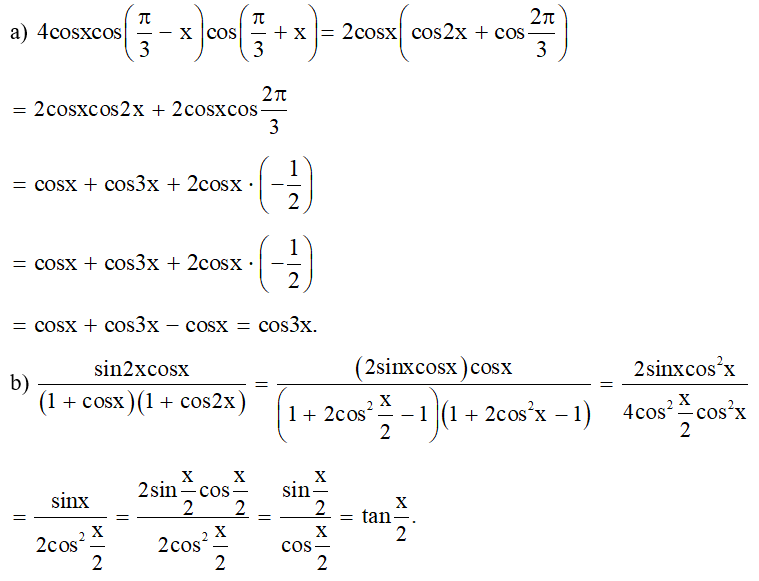
c) sinx(1 + 2cos2x + 2cos4x + 2cos6x)

= sinx + 2sinxcos2x + 2sinxcos4x + 2sinxcos6x

= sinx + [sin(‒x) + sin3x] + [sin(‒3x) + sin5x] + [sin(‒5x) + sin7x]

= sinx + (‒sinx + sin3x) + (‒sin3x + sin5x) + (‒sin5x + sin7x)

= sin7x.