Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng: a) Tia CA là tia phân giá
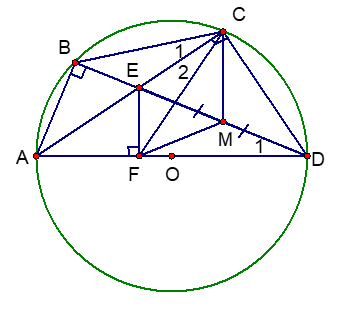
Cho tứ giác ABCD nội tiếp nửa đường tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Kẻ EF vuông góc với AD. Gọi M là trung điểm của DE. Chứng minh rằng:
a) Tia CA là tia phân giác của góc BCF