Cho tứ diện ABCD. Gọi G và H lần lượt là trọng tâm của hai tam giác ABC và ACD. Chứng minh rằng GH // (BCD).

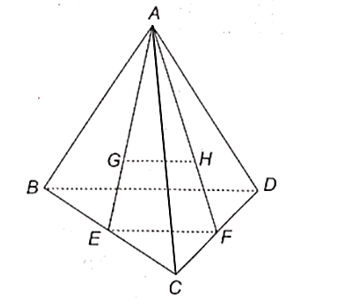
Gọi E, F lần lượt là trung điểm của các cạnh BC, CD.

Vì G là trọng tâm của tam giác ABC, nên A, G, E thẳng hàng và $\frac{AG}{AE}=\frac{2}{3}$.

Tương tự có A, H, F thẳng hàng và $\frac{AH}{AF}=\frac{2}{3}$.

Do đó $\frac{AG}{AE}=\frac{AH}{AF}$.

Theo định lí Thalès đảo, suy ra tam giác AEF có GH // EF.

Mà E ∈ BC ⊂ (BCD) và F ∈ CD ⊂ (BCD) nên EF ⊂ (BCD).

Vậy GH // (BCD).