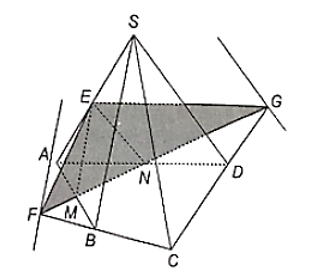
Cho hình chóp tứ giác S.ABCD và E là một điểm bất kì thuộc cạnh SA. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng SB, SD. Gọi M, N lần lượt là giao điểm của (P) và các cạnh AB, AD.

a) Chứng minh rằng EM // SB và EN // SD.

a) Vì M, N lần lượt là giao điểm của (P) và các cạnh AB, AD và E thuộc SA, đồng thời E thuộc mặt phẳng (P) nên EM, EN là các giao tuyến của các mặt phẳng (SAB), (SAD) với mặt phẳng (P).

Mặt phẳng (SAB) chứa đường thẳng SB song song với (P) nên giao tuyến của hai mặt phẳng đó song song với SB, suy ra EM // SB. Tương tự có EN // SD.