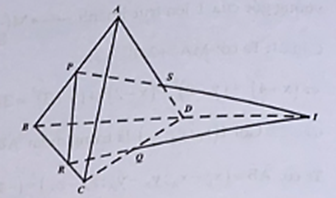
Cho tứ diện ABCD. Các điểm P, Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC . Gọi S là giao điểm của mặt phẳng (PQR) và cạnh AD.

A. 2

B. 1

C. $\frac{1}{2}$

D. $\frac{1}{3}$

Trả lời

Chọn A

Gọi I là giao điểm của BD và RQ. Nối P với I, cắt AD tại S. Xét tam giác BCD bị cắt bởi IR, ta có $\frac{\text{DI}}{\text{IB}}.\frac{\text{BR}}{\text{RC}}.\frac{\text{CQ}}{\text{QD}}=1\iff \frac{\text{DI}}{\text{IB}}\mathrm{.2.1}=1\iff \frac{\text{DI}}{\text{IB}}=\frac{1}{2}$.

Xét tam giác ABD bị cắt bởi PI, ta có $\frac{\text{AS}}{\text{SD}}.\frac{\text{DI}}{\text{IB}}.\frac{\text{BP}}{\text{PA}}=1\iff \frac{\text{SA}}{\text{SD}}.\frac{1}{2}.1=1\iff \frac{\text{SA}}{\text{SD}}=2$.