Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP)
572
06/12/2023
Luyện tập trang 30 Toán 11 Tập 2: Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.
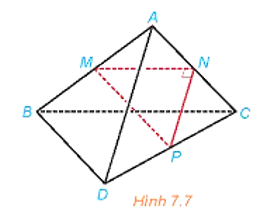
Trả lời
Xét tam giác ABC có M là trung điểm của AB, N là trung điểm của AC nên MN là đường trung bình của tam giác ABC, suy ra MN // BC.
Xét tam giác ACD có N là trung điểm của AC, P là trung điểm của CD nên NP là đường trung bình của tam giác ACD, suy ra NP // AD.
Khi đó (AD, BC) = (NP, MN) = .
Do tam giác MNP vuông tại N nên .
Vậy AD và BC vuông góc với nhau.
Nếu D Î (ABC) thì A Î (MNP) (vô lí).
Do đó D Ï (ABC) nên AD và BC chéo nhau.
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

