Cho tam giác ABC vuông tại A, tia Cx nằm giữa hai tia CA và CB. Vẽ đường tròn (O) có O thuộc cạnh AB, tiếp xúc với cạnh CB tại M và tiếp xúc với tia Cx tại N. Chứng minh rằng: a) Tứ giác MON
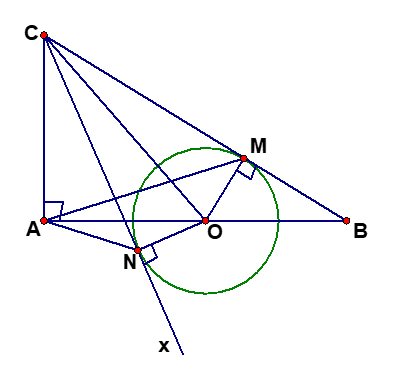
Cho tam giác ABC vuông tại A, tia Cx nằm giữa hai tia CA và CB. Vẽ đường tròn (O) có O thuộc cạnh AB, tiếp xúc với cạnh CB tại M và tiếp xúc với tia Cx tại N. Chứng minh rằng:
a) Tứ giác MONC nội tiếp được đường tròn.