Cho tam giác ABC vuông cân đỉnh A. Đường tròn đường kính AB cắt BC tại D Điểm M bất kỳ trên đoạn AD kẻ MH, MI lần lượt vuông góc với 1) Chứng minh: Tứ giác MDCI nội tiếp 2) Chứng mi
88
07/05/2024
Cho tam giác ABC vuông cân đỉnh A. Đường tròn đường kính AB cắt BC tại D 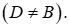 Điểm M bất kỳ trên đoạn AD kẻ MH, MI lần lượt vuông góc với
Điểm M bất kỳ trên đoạn AD kẻ MH, MI lần lượt vuông góc với 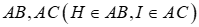
1) Chứng minh: Tứ giác MDCI nội tiếp
2) Chứng minh: 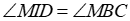
3) Kẻ 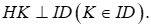 Chứng minh K, M, B thẳng hàng
Chứng minh K, M, B thẳng hàng
4) Khi M di động trên đoạn AD. Chứng minh rằng đường thẳng HK luôn đi qua một điểm cố định
Trả lời
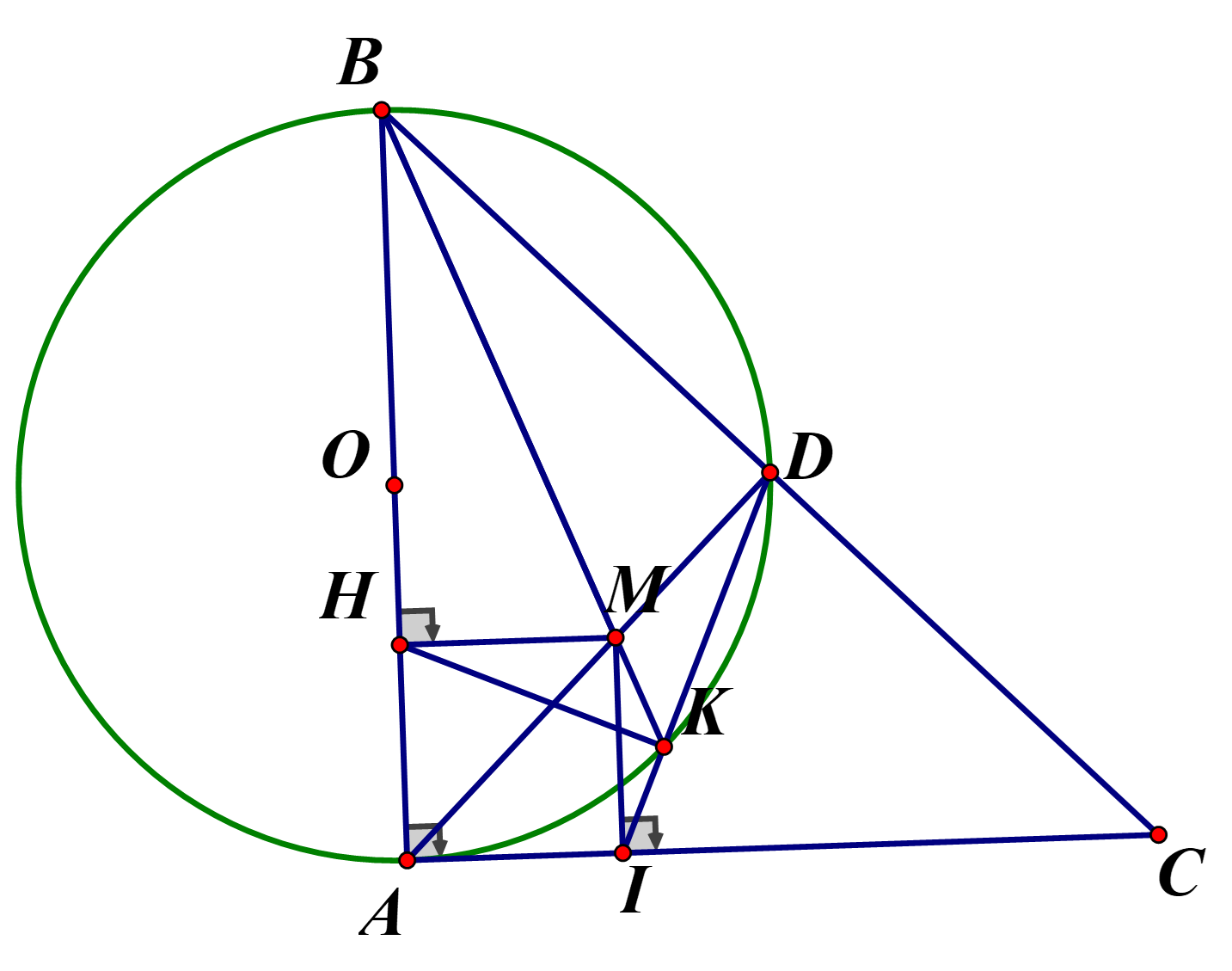
\(a)MI \bot AC,MD \bot BC \Rightarrow \angle MIC + \angle MDC = 90^\circ + 90^\circ = 180^\circ \)
\( \Rightarrow MDCI\)là tứ giác nội tiếp
\(b)MDCI\)là tứ giác nội tiếp \( \Rightarrow \angle MID = \angle MCD\left( 1 \right);\)
\(\Delta ABC\)vuông cân \( \Rightarrow \angle ABD = 45^\circ \Rightarrow \Delta ABD\)cũng vuông cân
\( \Rightarrow \angle BAD = 45^\circ \Rightarrow \angle BAD = \angle DAC = 45^\circ \Rightarrow AD\)là tia phân giác của \(\angle BAC\)
\( \Rightarrow \Delta BAC\)cân tại A, có \(AD\)là phân giác nên đồng thời là trung trực
\( \Rightarrow MB = MC \Rightarrow \angle MBD = \angle MCD\left( 2 \right)\)
\(\left( 1 \right),\left( 2 \right) \Rightarrow \angle MID = \angle MBD = \angle MBC(dfcm)\)
c) \(HK \bot ID \Rightarrow \angle HAI + \angle IKH = 180^\circ \Rightarrow AHKI\)nội tiếp
mà \(AHMI\)cũng nội tiếp (vì \(\angle AHM = 90^\circ = \angle AIM)\)\( \Rightarrow A,H,M,K,I\)cũng thuộc đường tròn
\( \Rightarrow AMKI\)nội tiếp \( \Rightarrow \angle AMK = 90^\circ - \angle HAM = 45^\circ \)
Lại có : \(\angle DIC = \angle DMC = \angle BMD\)(MD là trung trực \(BC)\)
\( \Rightarrow \angle HMA + \angle HMB + \angle AMK = \angle HMB + \angle BMD + \angle HMA = \angle AMD = 180^\circ \)
\( \Rightarrow \angle BMK = 180^\circ \Rightarrow B,M,K\)thẳng hàng
![]() Điểm M bất kỳ trên đoạn AD kẻ MH, MI lần lượt vuông góc với
Điểm M bất kỳ trên đoạn AD kẻ MH, MI lần lượt vuông góc với ![]()
![]()
![]() Chứng minh K, M, B thẳng hàng
Chứng minh K, M, B thẳng hàng
