Cho tam giác ABC nội tiếp đường tròn tâm O. Các đỉnh B, C cố định còn đỉnh A thay đổi trên đường tròn đó

Bài 1.32 trang 33 Chuyên đề Toán 11: Cho tam giác ABC nội tiếp đường tròn tâm O. Các đỉnh B, C cố định còn đỉnh A thay đổi trên đường tròn đó. Vẽ hình bình hành ABCD. Chứng minh rằng điểm D luôn thuộc một đường tròn cố định.

Trả lời

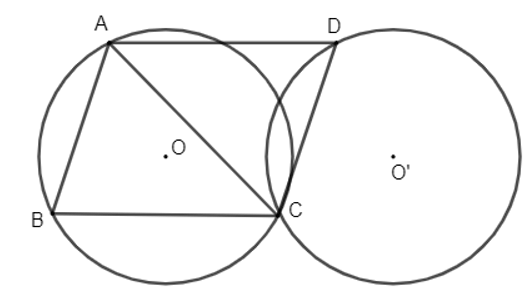
Vì ABCD là hình bình hành nên $\overrightarrow{AD}=\overrightarrow{BC}$.

Do B, C cố định nên vectơ $\overrightarrow{BC}$ cố định.

Khi đó ta có phép tịnh tiến theo vectơ $\overrightarrow{BC}$ biến điểm A thành điểm D. Mặt khác, A thuộc đường tròn tâm O ngoại tiếp tam giác ABC nên D thuộc đường tròn tâm O' cố định là ảnh của đường tròn tâm O qua phép tịnh tiến theo vectơ $\overrightarrow{BC}$. Ở đó, bán kính hai đường tròn bằng nhau và O' là ảnh của O qua phép tịnh tiến theo vectơ $\overrightarrow{BC}$ được xác định bởi $\overrightarrow{OO\text{'}}=\overrightarrow{BC}$.

Xem thêm các bài giải Chuyên đề Toán lớp 11 Kết nối tri thức hay, chi tiết khác: