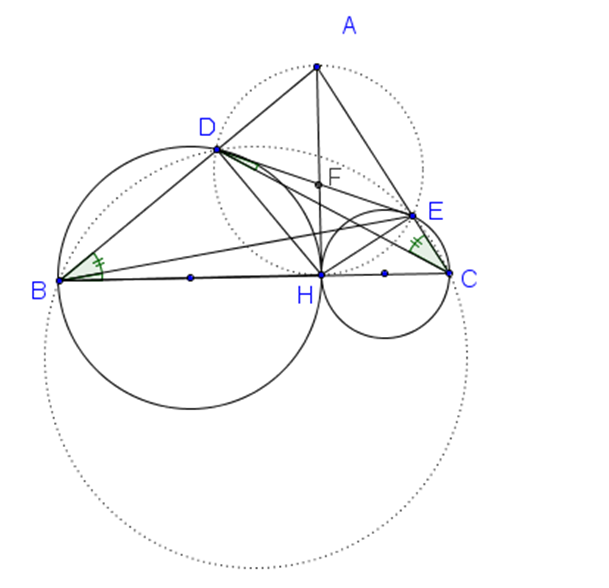
Cho tam giác ABC; H là chân đường cao kẻ từ A. Đường tròn đường kính HB cắt AB tại điểm thứ hai là D.
Cho tam giác ABC; H là chân đường cao kẻ từ A. Đường tròn đường kính HB cắt AB tại điểm thứ hai là D. Đường tròn đường kính HC cắt AC tại điểm thứ hai là E.
a) Chứng minh 4 điểm A, D, H, E cùng nằm trên một đường tròn.