Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho
4
30/10/2024
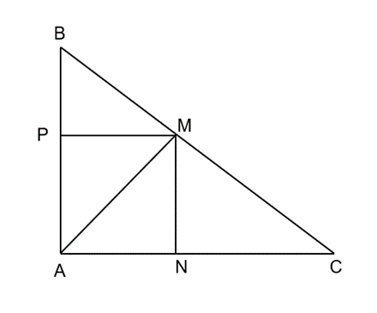
Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.
a) Chứng minh rằng ΔBMP ∽ ΔMCN.
Trả lời
a) Vì BM = 4 cm; BC = 10 cm nên MC = 6 cm.
Ta thấy 62 + 82 = 102 = 100 hay AB2 + AC2 = BC2 nên tam giác ABC vuông tại A.
Lại có MN // AB (cùng vuông góc với AC) và MP // AC (cùng vuông góc với AB).
Tam giác BMP vuông tại P và tam giác MCN vuông tại N có (MP // AC và hai góc ở vị trí đồng vị) nên ∆BMP ∽ ∆MCN.