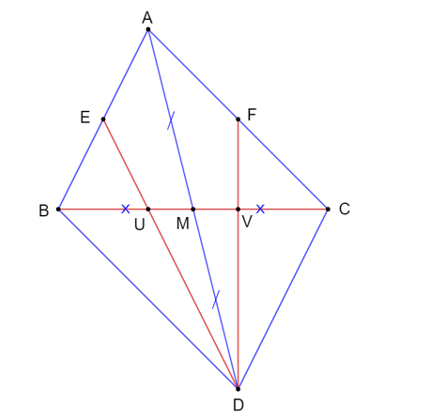
Cho tam giác ABC có M là trung điểm của cạnh BC và D là điểm sao cho M là trung điểm của AD. Đường thẳng qua D và trung điểm E của AB cắt BC tại U, đường thẳng qua D và trung điểm F của AC cắt BC tại V. Khẳng định nào sau đây là sai?

A. BU = UV;

B. BU = VC;

Hướng dẫn giải:

Đáp án đúng là: C

⦁ Tam giác BAC có M là trung điểm của BC nên suy ra MB = MC (1)

Xét ∆ABD có U là giao của hai đường trung tuyến BM và DE nên U là trọng tâm của ∆ABD.

Suy ra $BU=\frac{2}{3}BM$          (2)

Từ đó ta có: $UM=BM-BU=BM-\frac{2}{3}BM=\frac{1}{3}BM$ (3)

Do đó khẳng định C là sai. Đến đây ta có thể chọn phương án C.

⦁ Xét phương án D:

Xét ∆ACD có V là giao của hai đường trung tuyến CM và DF nên V là trọng tâm của ∆ACD.

Suy ra $CV=\frac{2}{3}CM$ (4)

Từ đó ta có: $MV=CM-CV=CM-\frac{2}{3}CM=\frac{1}{3}CM$ (5)

Từ (1), (3), (5) ta có: $UV=UM+MV=\frac{1}{3}MB+\frac{1}{3}MC=\frac{2}{3}MB$ (6)

Do đó khẳng định D là đúng.

⦁ Xét phương án A và B:

Từ (1), (2), (4), (6) ta có: $BU=UV=VC=\frac{2}{3}MB$.

Do đó khẳng định A và B là đúng.

Vậy ta chọn phương án C.