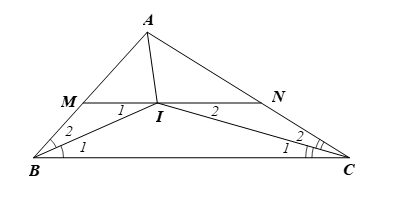
Cho ΔABC có I là giao điểm của hai tia phân giác của góc A và B. Qua I kẻ đường thẳng

C. MN < BM + CN;

Trả lời

Hướng dẫn giải:

Đáp án đúng là: A

Xét ∆ABC có I là giao điểm của hai tia phân giác $\widehat{A}$ và $\widehat{B}$ nên CI là tia phân giác của $\widehat{C}$

Vì MN // BC nên ${\widehat{C}}_1={\widehat{I}}_2$ (hai góc so le trong)

Mà ${\widehat{C}}_1=\widehat{C_2}$ nên ${\widehat{C}}_2={\widehat{I}}_2$

Do đó ΔNIC cân tại N nên NC = NI.   (1)

Tương tự, ta có: MB = MI.        (2)

Từ (1) và (2) ta có: MI + IN = BM + CN hay MN = BM + CN.