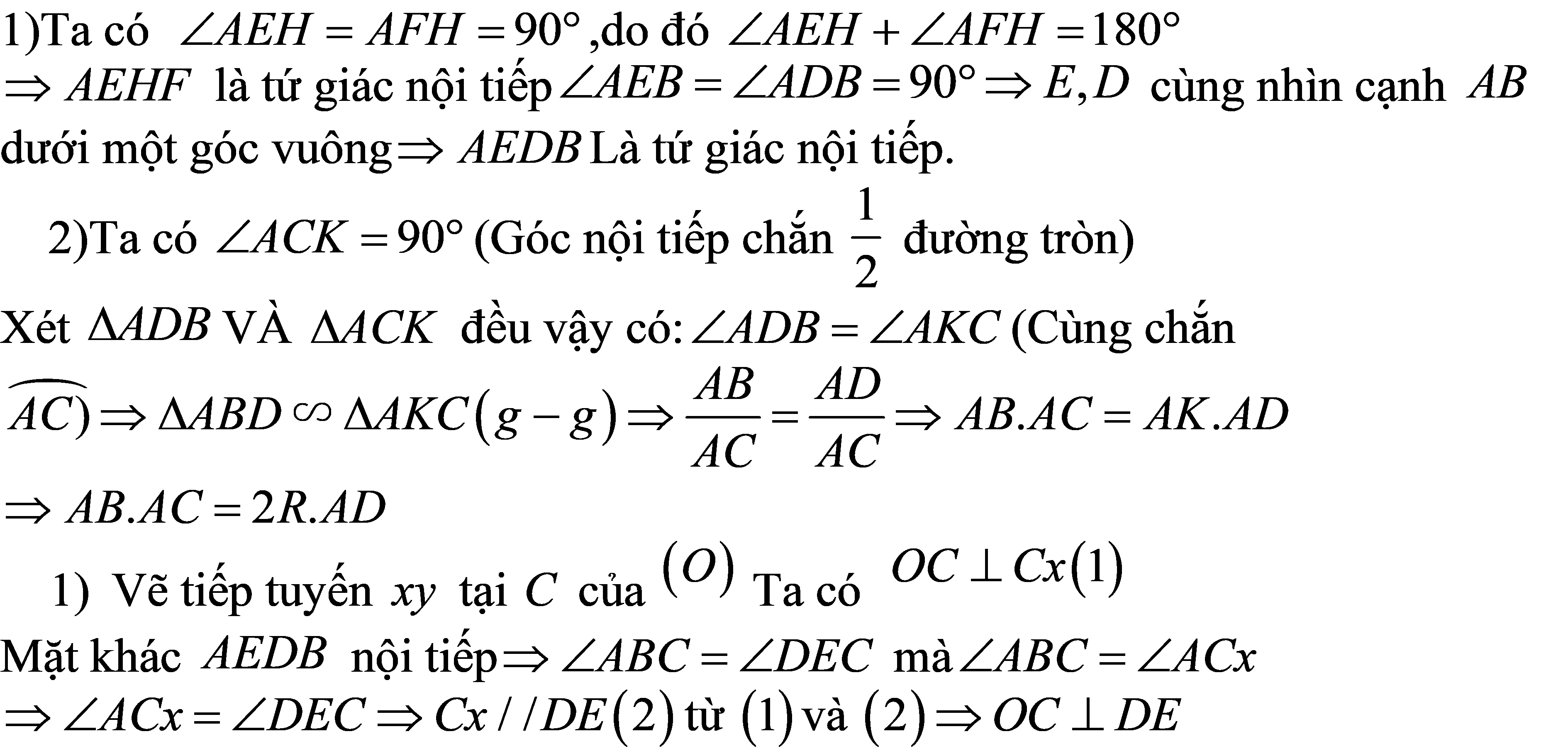Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC. 1 Chứng minh rằng AEHF và AEDF là
Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
1 Chứng minh rằng AEHF và AEDF là các tư giác nội tiếp đường tròn.
2 Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKC đồng dạng với nhau. Suy ra AB. AC = 2R. AD
3 Chứng minh rằng OC vuông góc với DE.