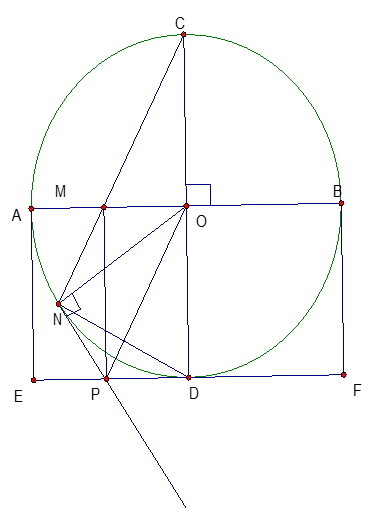
Cho (O; R)  có hai đường kính AB và CD vuông góc nhau. Trên đoạn thẳng AB lấy điểm M (khác O) đường thẳng CM cắt đường tròn (O) tại điểm thứ hai N , đường thẳng vuông góc với AB tại M cắt tiếp tuyến tại N của đường tròn ở điểm P. Chứng minh rằng :

a) Ta có $\widehat{OMP}=1v$ (gt)

     $\widehat{ONP}=1v$ (T/C của hai tiếp tuyến )

=> Hai điểm C, M cùng nhìn đoạn thẳng OP dưới một góc vuông