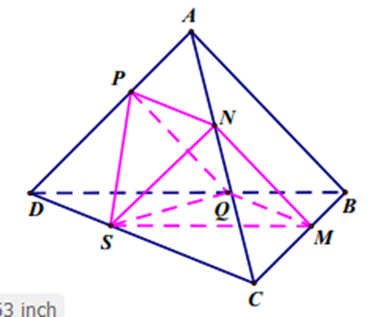
Cho khối tứ diện ABCD có thể tích bằng 27. Điểm M di động trên đoạn thẳng BC (M khác B,C), điểm S di động trên đường thẳng CD.
Cho khối tứ diện ABCD có thể tích bằng 27. Điểm M di động trên đoạn thẳng BC (M khác B,C), điểm S di động trên đường thẳng CD. Một mặt phẳng đi qua M, song song với hai đường thẳng AB, CD, đồng thời cắt AC,AD, BD lần lượt tại N,P,Q. Gọi V là thể tích của khối chóp S.MNPQ khi M, N thay đổi thì giá trị lớn nhất của V bằng