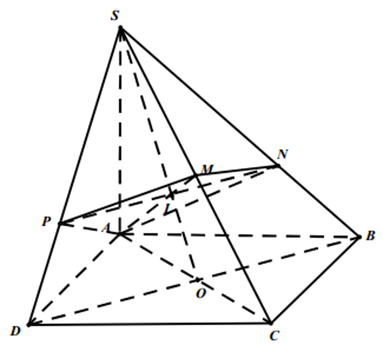
Cho khối chóp tứ giác S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC , mặt phẳng (P) chứa AM và song song BD chia khối chóp thành hai khối đa diện, gọi V
Cho khối chóp tứ giác S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC , mặt phẳng (P) chứa AM và song song BD chia khối chóp thành hai khối đa diện, gọi V, là thể tích khối đa diện có chứa đỉnh S, V, là thể tích khối đa diện chứa đáy ABCD . Tỉ số là
A.
B.
C.
D.