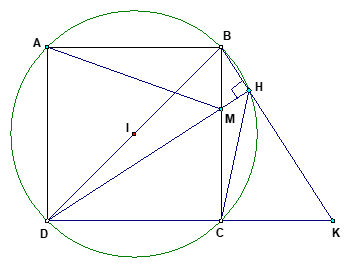
Cho hình vuông ABCD, lấy một điểm M bất kỳ trên cạnh BC (M khác B và C). Qua B kẻ đường thẳng vuông góc với đường thẳng DM tại H, kéo dài BH cắt đường thẳng DC tại K.

a) Chứng minh tứ giác BHCD nội tiếp đường tròn. Xác định tâm I  của đường tròn đó.

a) Ta có $\widehat{BCD}={90}^0$ (vì ABCD là hình vuông)

          $\widehat{BHD}={90}^0$ (vì $BH\perp DM$)

=> H, C cùng thuộc đường tròn đường kính BD

Vậy tứ giác BHCD nội tiếp được đường tròn đường kính BD, có tâm I là trung điểm đoạn BD.