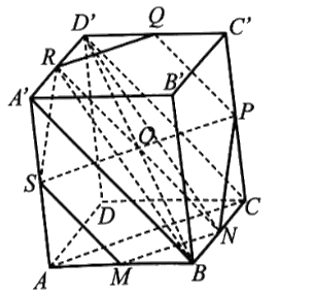
a) Ta có S và P lần lượt là trung điểm của AA' và CC'.
Suy ra .
Mà AA' = CC' và AA' // CC' (do ABCD.A'B'C'D' là hình hộp)
Nên AS = CP và AS // CP. Do đó, tứ giác ASPC là hình bình hành.
Suy ra AC // SP.
Mặt khác MN // AC (do MN là đường trung bình của tam giác ABC).
Khi đó, MN // SP.
Vậy M, N, P, S cùng thuộc một mặt phẳng.
Ta cũng chứng minh được PQ // CD', CD' // BA', BA' // MS nên PQ // MS.
Do đó Q ∈ (MNPS).
Tương tự ta có QR // MN nên R ∈ (MNPS).
Vậy sáu điểm M, N, P, Q, R, S cùng thuộc một mặt phẳng.
b) Gọi O là giao điểm của các đường chéo hình hộp ABCD.A'B'C'D'.
Khi đó, O là trung điểm của các đường chéo BD', B'D, AC', A'C.
Ta có tứ giác BND'R là hình bình hành, nên hai đường chéo BD', NR cắt nhau tại trung điểm O của mỗi đường.
Tương tự, ta chứng minh được QM, PS đều nhận O là trung điểm.
Vậy các đoạn thẳng MQ, NR, PS cắt nhau tại trung điểm của mỗi đoạn.