Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA', BB', CC', DD'. Chứng minh rằng bốn điểm
18
08/10/2024
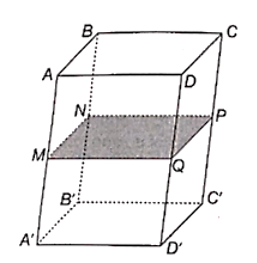
Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AA', BB', CC', DD'. Chứng minh rằng bốn điểm M, N, P, Q đồng phẳng và MNPQ là hình bình hành.
Trả lời
Vì M, N lần lượt là trung điểm của hai cạnh AA', BB' của hình bình hành ABB'A' nên ta có MN // AB, suy ra MN // (ABCD).
Tương tự NP // (ABCD), do đó (MNP) // (ABCD).
Lập luận tương tự suy ra (NPQ) // (ABCD).
Qua điểm N có hai mặt phẳng (MNP) và (NPQ) cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng (MNP) và (NPQ) trùng nhau, tức là bốn điểm M, N, P, Q đồng phẳng.
Ngoài ra từ M, N lần lượt là trung điểm của hai cạnh AA', BB' của hình bình hành ABB'A' ta suy ra được MN = AB.
Do đó, MN // AB và MN = AB.
Tương tự, ta chứng minh được PQ // CD và PQ = CD.
Mà AB // CD và AB = CD (do ABCD là hình bình hành).
Khi đó, MN // PQ và MN = PQ nên tứ giác MNPQ là hình bình hành.