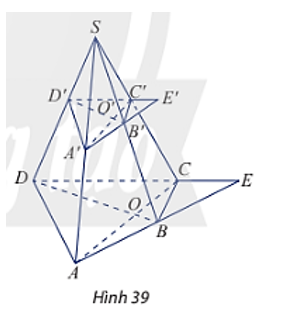
Cho hình chóp S.ABCD. Trên các cạnh bên của hình chóp lấy lần lượt các điểm A’, B’, C’, D’. Cho biết AC cắt BD tại O, A’C’ cắt B’D’ tại O’, AB cắt CD tại E và A’B’ cắt D’C’ tại E’ (Hình 39). Chứng minh rằng:

a) S, O’, O thẳng hàng;

a) +) Ta có  $\left.\begin{array}{l}S\in \left(SAC\right)\\ S\in \left(SBD\right)\end{array}\right\}\Rightarrow S\in \left(SAC\right)\cap \left(SBD\right)$

Ta lại có: O là giao điểm của AC và BD nên

 $\left.\begin{array}{l}O\in AC\subset \left(SAC\right)\\ O\in BD\subset \left(SBD\right)\end{array}\right\}\Rightarrow O\in \left(SAC\right)\cap \left(SBD\right)$

Suy ra  $\left(SAC\right)\cap \left(SBD\right)=SO$.

+) Ta có  $\left.\begin{array}{l}S\in \left(SA\text{'}C\text{'}\right)\\ S\in \left(SB\text{'}D\text{'}\right)\end{array}\right\}\Rightarrow S\in \left(SA\text{'}C\text{'}\right)\cap \left(SB\text{'}D\text{'}\right)$

Ta lại có: O’ là giao điểm của A’C’ và B’D’ nên

 $\left.\begin{array}{l}O\text{'}\in A\text{'}C\text{'}\subset \left(SA\text{'}C\text{'}\right)\\ O\text{'}\in B\text{'}D\text{'}\subset \left(SB\text{'}D\text{'}\right)\end{array}\right\}\Rightarrow O\in \left(SA\text{'}C\text{'}\right)\cap \left(SB\text{'}D\text{'}\right)$

Suy ra  $\left(SA\text{'}C\text{'}\right)\cap \left(SB\text{'}D\text{'}\right)=SO\text{'}$.

+) Mặt khác mặt phẳng (SA’C’) cũng chính là mặt phẳng (SAC), mặt phẳng (SB’D’) cũng chính là mặt phẳng (SBD) do đó SO’ trùng SO. Vì vậy S, O’, O thẳng hàng.