Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D). a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD), (EFG) v
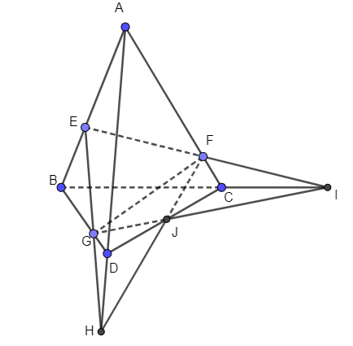
Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D).
a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD), (EFG) và (ACD).