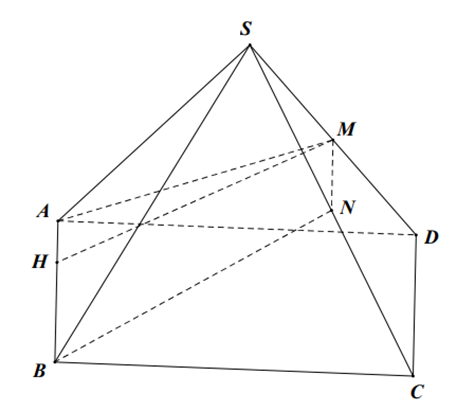
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, các cạnh bên bằng a căn 2. Gọi M là trung điểm của SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (ABM).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, các cạnh bên bằng a√2. Gọi M là trung điểm của SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (ABM).
A. 3√15a216
B. 3√5a216
C. 3√5a28
D. √15a216