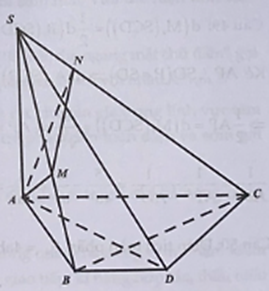
Cho hình chóp S.ABC có SA vuông góc với đáy, SA = 2BC và góc $\widehat{BAC}={120}^{°}$. Hình chiếu vuông góc của A lên các đoạn SB và SC lần lượt là M và N. Tính góc giữa hai mặt phẳng (ABC) và (AMN).

Kẻ đường kính AD của đường tròn ngoại tiếp $\Delta \text{ABC}$ nên $\widehat{\text{ABD}}=\widehat{\text{ACD}}={90}^{°}$.

Ta có $\left\{\begin{array}{l}BD\perp BA\\ BD\perp SA\end{array}\Rightarrow BD\perp \left(SAB\right)\right.$ hay $BD\perp AM$ và $\text{AM}\perp \text{SB}$ hay $\text{AM}\perp \left(\text{SBD}\right)\Rightarrow \text{AM}\perp \text{SD}$.

Chứng minh tương tự ta được $\text{AN}\perp \text{SD}$.

Suy ra $\text{SD}\perp \left(\text{AMN}\right)$, mà $\text{SA}\perp \left(\text{ABC}\right)\Rightarrow \left(\right(\text{ABC}),(\text{AMN}\left)\right)=(\text{SA},\text{SD})=\widehat{\text{DSA}}$.

Ta có $BC=2R\sin A=AD\cdot \frac{\sqrt{3}}{2}\Rightarrow SA=2BC=AD\sqrt{3}$.