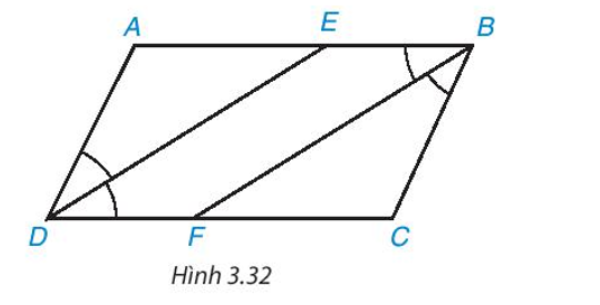
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F (H.3.32).
a) Chứng minh hai tam giác ADE và CBF là những tam giác cân, bằng nhau.
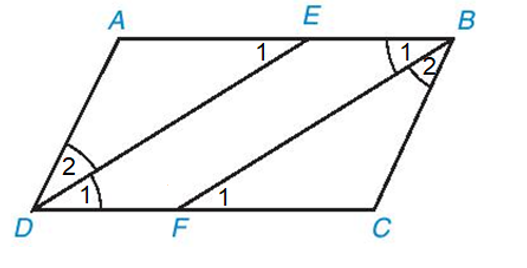
a) Vì ABCD là hình bình hành nên AB // CD hay BE // DF.
Vì DE là tia phân giác của ^ADC nên ˆD1=ˆD2.
Mà ˆD1=ˆE1 (BE // DF, hai góc so le trong) nên ˆD2=ˆE1.
Suy ra tam giác ADE cân tại A.
Tương tự ta cũng chứng minh được: tam giác BCF cân tại C.
Vì ABCD là hình bình hành nên AD = BC; ˆA=ˆC; ^ADC=^ABC.
Vì AE là tia phân giác ^ADC; BF là tia phân giác ^ABC nên
ˆB1=ˆB2; ˆD1=ˆD2 mà ^ADC=^ABC.
Do đó ˆB1=ˆB2=ˆD1=ˆD2.
Xét ∆ADE và ∆CBF có:
ˆA=ˆC (chứng minh trên);
AD = BC (chứng minh trên);
ˆB2=ˆD2 (chứng minh trên).
Do đó ∆ADE = ∆CBF (g.c.g).