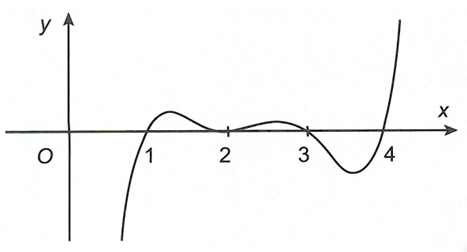
Cho hàm số y=f(x) là hàm đa thức bậc 6 thỏa mãn 3f(1)-2<0 và 3f(a)-a^3+3a>0, với a >2 . Đồ thị hàm số y=f(x) như hình vẽ.
35
23/04/2024
Cho hàm số y=f(x) là hàm đa thức bậc 6 thỏa mãn 3f(1)−2<0 và 3f(a)−a3+3a>0,∀a>2 . Đồ thị hàm số y=f' như hình vẽ.
Số đường tiệm cận đứng của đồ thị hàm số là
A. 0
B. 2
C. 1
D. 3
Trả lời
Hướng dẫn giải
Đặt . Điều kiện .
Ta có , .
Đặt , ta được . (*)
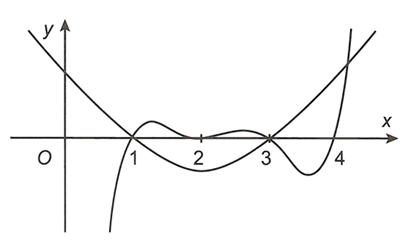
Vẽ đồ thị hàm số vào cùng hệ trục có đồ thị hàm số ta được hình vẽ sau
Dựa vào đồ thị ta thấy (*) có ba nghiệm là .
Suy ra phương trình có nghiệm đơn .
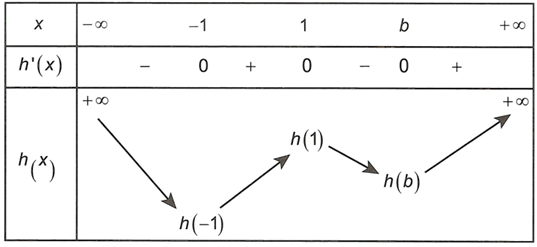
Ta có bảng biến thiên của như sau
Vì và với mọi nên phương trình có hai nghiệm phân biệt .
Vậy đồ thị hàm số có hai tiệm cận đứng.
Chọn B.