Cho hàm số y= x+1/ x-1 có đồ thị (C). Gọi A, B là hai điểm nằm trên hai nhánh của (C) và các tiếp tuyến của (C) tại A, B cắt các đường tiệm cận ngang
Cho hàm số y=x+1x−1 có đồ thị (C). Gọi A, B là hai điểm nằm trên hai nhánh của (C) và các tiếp tuyến của (C) tại A, B cắt các đường tiệm cận ngang và tiệm cận đứng lần lượt tại các cặp M, N và P, Q. Diện tích tứ giác MNPQ nhỏ nhất bằng
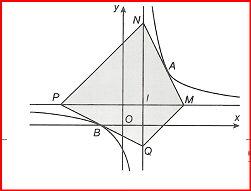
A. 16
B. 32
C. 8
D. 4
