Cho hàm số g(x)=2020/h(x)-m^2-m với h(x)=mx^4+nx^3+px^2+qx . (m,n,p,q thuộc R, m khác 0) ,
41
23/04/2024
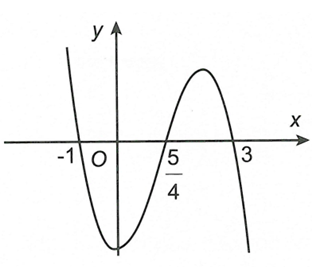
Cho hàm số với . , . Hàm số có đồ thị như hình vẽ bên dưới.
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số có hai tiệm cận đứng?
A. 2
B. 11
C. 71
D.2019
Trả lời
Hướng dẫn giải
Từ đồ thị suy ra và nên do
Đồ thị có hai đường tiệm cận đứng phương trình có hai nghiệm phân biệt có hai nghiệm phân biệt.
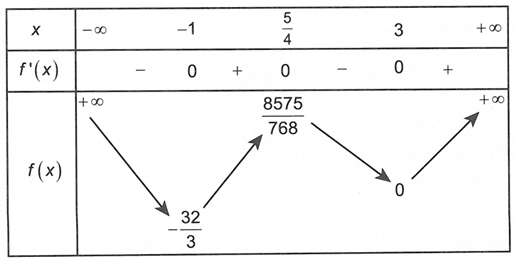
Đặt .
Ta có bảng biến thiên của như sau
Vì nên .
Vậy có 11 số nguyên m.
Chọn B.