Cho hàm số f(x) có đạo hàm $f^{\text{'}}\left(x\right)=x(x-1){(x+2)}^{2021}{(x+3)}^{2020},\forall x\in ℝ$. Số điểm cực trị của hàm số đã cho là bao nhiêu?

Phương trình f'(x) = 0 có các nghiệm $x=0;x=1;x=-2;x=3$.

Bảng xét dấu của f'(x) (ta có thể đưa về việc xét dấu của biểu thức $g\left(x\right)=x(x-1)(x+2)$)

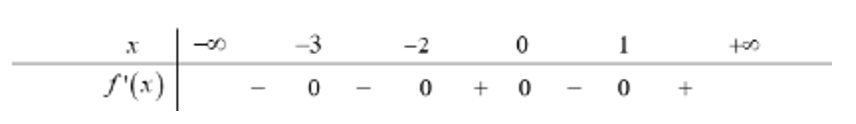
Vậy hàm số có 3 điểm cực trị.