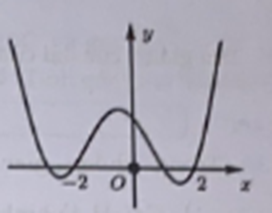
Cho hàm số bậc bốn y = f(x) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số  g(x) = f(x3 - 3x) là

Cho hàm số bậc bốn y = f(x) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số  g(x) = f(x³ - 3x) là

A. 5

B. 7

C. 9

D. 11

Trả lời

Từ đồ thị ta có bảng xét dấu y' = f'(x) của hàm sồ y = f(x) như sau

Với a $\in (-\infty ;-2),b\in (-2;0),c\in (0;2)$. Ta có $g^{\text{'}}\left(x\right)=\left(3x^2-3\right)f^{\text{'}}\left(x^3-3x\right)$.

$g^{\text{'}}\left(x\right)=0\iff \left[\begin{array}{l}3x^2-3=0\\ f^{\text{'}}(x^3-3x)=0\end{array}\iff \left[\begin{array}{l}x=\pm 1\\ x^3-3x=a\\ x^3-3x=b\\ x^3-3x=c\end{array}\right.\right.\text{. }$

Xét hàm số $\text{h}\left(\text{x}\right)={\text{x}}^3-3\text{x}$.

Ta có .

Bảng biễn thiên của h(x):

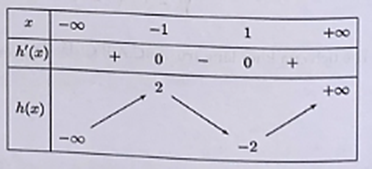
Từ bảng biến thiên trên ta có:

Hướng dẫn giải để số 5

+) Phương trình $x^3-3x=a$ với $a\in (-\infty ;-2)$ có một nghiệm x₁ nhỏ hơn -1 .

+) Phương trình $x^3-3x=b$ với $b\in (-2;0)$ có ba nghiệm phân biệt $x_2,x_3,x_4$ khác $\pm 1$ và khác x₁

+) Phương trình $x^3-3x=c$ với $c\in (0;2)$ có ba nghiệm phân biệt $x_5,x_6,x_7$ khác $\pm 1,x_1,x_2,x_3$ và x₄

Như vậy phương trình g'(x) = 0 có 9 nghiệm phân biệt gồm $x_1,x_2,x_3,x_4,x_5,x_6,x_7,-1,1$ nên hàm số $\text{g}\left(\text{x}\right)=\text{f}\left({\text{x}}^3-3\text{x}\right)$ có 9 điểm cực trị.