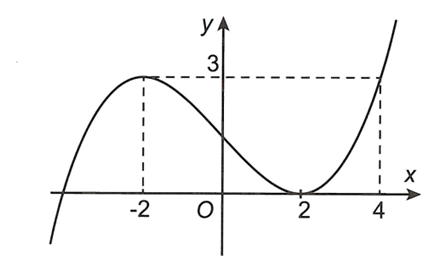
Cho hàm số bậc ba $f\left(x\right)=a{x}^3+b{x}^2+cx+d\left(a,b,c,d\in ℝ\right)$  có đồ thị như hình vẽ dưới đây.

Đồ thị hàm số $g\left(x\right)=\frac{1}{f\left(4-x^2\right)-3}$  có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

Hướng dẫn giải

Đặt $t=4-x^2$ , ta có khi $x\to \pm \infty$  thì $t\to -\infty$ .

Khi đó $\underset{x\to \pm \infty }{\lim }g\left(x\right)=\underset{t\to -\infty }{\lim }\frac{1}{f\left(t\right)-3}=0$  nên $y=0$  là tiệm cận ngang của đồ thị hàm số $g\left(x\right)$ .

Mặt khác $f\left(4-x^2\right)-3=0\iff f\left(4-x^2\right)=3\iff \left[\begin{array}{l}4-x^2=-2\\ 4-x^2=4\end{array}\right.\iff \left[\begin{array}{l}x=\pm \sqrt{6}\\ x=0\end{array}\right.$

$\Rightarrow$ Đồ thị hàm số $g\left(x\right)$  có ba đường tiệm cận đứng.

Vậy đồ thị hàm số $g\left(x\right)$  có bốn đường tiệm cận.

Chọn C.