Cho hàm số bậc ba f(x)= ã^3+bx^2+cx+d có đồ thị như hình vẽ. Đồ thị hàm số g(x)= (x^2-3x+2) căn 2x+1/ ( x^4-5x^2+4)f(x)
Cho hàm số bậc ba có đồ thị như hình vẽ.
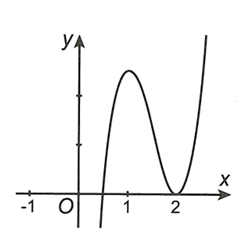
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?
A. 2
B. 6
C. 4
D. 3
Cho hàm số bậc ba có đồ thị như hình vẽ.

Đồ thị hàm số có bao nhiêu đường tiệm cận đứng?
A. 2
B. 6
C. 4
D. 3
Hướng dẫn giải
Điều kiện xác định .
Với điều kiện trên, ta có .
Khi đó số đường tiệm cận đứng của đồ thị hàm số là số nghiệm của phương trình thỏa mãn .
Dựa vào đồ thị ta thấy phương trình
(thỏa mãn điều kiện).
Vậy đồ thị hàm số có hai đường tiệm cận đứng.
Chọn A.