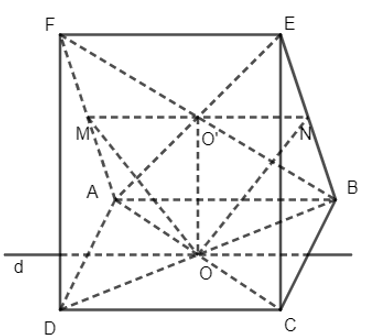
Cho hai hình bình hành ABCD và ABEF không nằm trong cùn một mặt phẳng. Gọi O và O’ lần lượt là tâm của ABCD và ABEF. a) Chứng minh đường thẳng OO’ song song với các mặt phẳng (CDEF), (ADF) và
41
17/08/2024
Cho hai hình bình hành ABCD và ABEF không nằm trong cùn một mặt phẳng. Gọi O và O’ lần lượt là tâm của ABCD và ABEF.
a) Chứng minh đường thẳng OO’ song song với các mặt phẳng (CDEF), (ADF) và (BCE).
Trả lời
a) Vì O là tâm hình bình hành ABCD nên O là trung điểm AC và BD, O’ là tâm của hình bình hành ABEF nên O’ là trung điểm AE và BF.
+) Ta có: OO’ // FD (tính chất đường trung bình trong tam giác BDF), mà FD ⊂ (CDEF). Do đó OO’ // (CDEF).
+) Ta lại có: FD ⊂ (ADF) nên OO’ // (ADF).
+) Ta có: OO’ // EC (tính chất đường trung bình trong tam giác ACE), mà EC ⊂ (BCE). Do đó OO’ // (BCE).