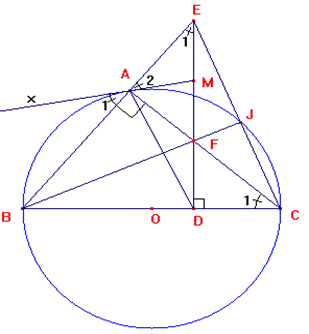
Cho đường tròn tâm O, đường kính BC, A là một điểm nằm trên đường tròn sao cho dây AB bé hơn dây AC. Trên đoạn OC lấy điểm D (D khác O, C). Từ D kẻ đường thẳng vuông góc với BC, đường thẳng này cắt hai đường thẳng BA và AC lần lượt tại E và F.

a) Ta có $B\widehat{A}C={90}^0$ (hệ quả góc nội tiếp)

              $B\widehat{D}F={90}^0$ (gt)

$\Rightarrow B\widehat{A}C+B\widehat{D}F={180}^0$

Vậy tứ giác ABDF nội tiếp.

Ta có $B\widehat{A}C={90}^0\Rightarrow E\widehat{A}C={90}^0$ (kề bù)

Mà $E\widehat{D}C={90}^0$

$\Rightarrow$ Tứ giác AECD nội tiếp.