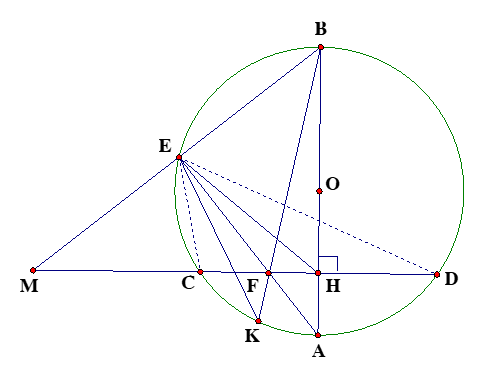
Cho đường tròn tâm O đường kính AB, dây CD vuông góc với AB tại H. Trên tia đối của tia CD, lấy một điểm M ở ngoài đường tròn (O).
Cho đường tròn tâm O đường kính AB, dây CD vuông góc với AB tại H. Trên tia đối của tia CD, lấy một điểm M ở ngoài đường tròn (O). Kẻ MB cắt đường tròn tại điểm E, AE cắt CD tại điểm F.
a. Chứng minh tứ giác BEFH nội tiếp một đường tròn.