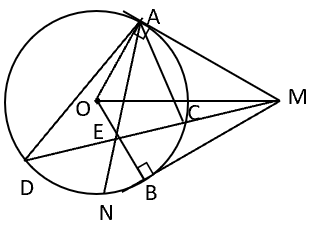
Cho đường tròn O, bán kính R. Từ một điểm M ở ngoài đường tròn (O) sao cho MO = 2R, ta kẽ hai tiếp tuyến MA và MB (A và B là tiếp điểm).
Cho đường tròn O, bán kính R. Từ một điểm M ở ngoài đường tròn (O) sao cho MO = 2R, ta kẽ hai tiếp tuyến MA và MB (A và B là tiếp điểm). Một cát tuyến bất kỳ qua M cắt đường tròn tại C và D . Kẻ tia phân giác của cắt dây CD tại E và đường tròn tại N.
a).Chứng minh tứ giác OAMB nội tiếp được.