Cho đường thẳng d và hai điểm phân biệt A, B. Điểm M thay đổi trên đường thẳng d. Gọi N là điểm đối xứng của M qua đường thẳng AB và P là trung điểm của đoạn thẳng BN. Chứng minh rằng P thuộc
27
29/07/2024
Cho đường thẳng d và hai điểm phân biệt A, B. Điểm M thay đổi trên đường thẳng d. Gọi N là điểm đối xứng của M qua đường thẳng AB và P là trung điểm của đoạn thẳng BN. Chứng minh rằng P thuộc một đường thẳng cố định.
Trả lời
Lời giải:
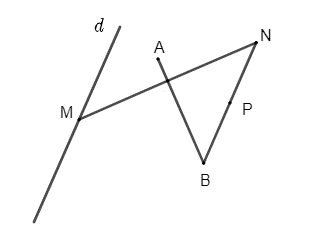
Vì N là điểm đối xứng của M qua đường thẳng AB nên ta có phép đối xứng trục AB biến điểm M thành điểm N.
Ta có P là trung điểm của BN nên \(\overrightarrow {BP} = \frac{1}{2}\overrightarrow {BN} \), do đó ta có phép vị tự tâm B, tỉ số \(\frac{1}{2}\) biến điểm N thành điểm P.
Như vậy, phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\,\frac{1}{2}} \right)}}\) biến điểm M thành điểm P.
Mặt khác M thuộc đường thẳng d cố định, A và B cố định, do đó P thuộc đường thẳng d' cố định là ảnh của đường thẳng d qua phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\,\frac{1}{2}} \right)}}\).
Vậy P thuộc một đường thẳng cố định.
