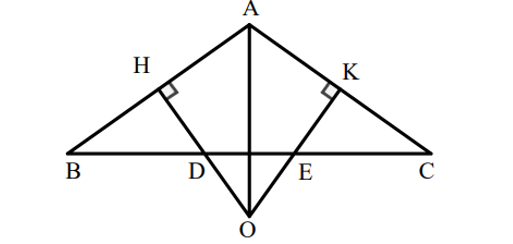
Cho ∆ABC cân tại A, góc A >90 độ, Các đường trung trực của AB và AC cắt nhau tại O và cắt BC lần lượt tại D và E.
15
16/11/2024
Cho ∆ABC cân tại A, ˆA>90° Các đường trung trực của AB và AC cắt nhau tại O và cắt BC lần lượt tại D và E. Khẳng định nào dưới đây là sai?
A. OA là đường trung trực của BC;
C. BD = DE = EC;
D. ∆ODE là tam giác cân.
Trả lời
Hướng dẫn giải:
Đáp án đúng là: C
Gọi O là giao điểm các đường trung trực của AB và AC.
Suy ra O nằm trên đường trung trực của BC.
Mà ∆ABC cân tại A nên AB = AC nên A nằm trên đường trung trực của BC.
Do đó AO là đường trung trực của BC.
Gọi H là trung điểm của AB nên
Gọi K là trung điểm của AC nên
Mà AB = AC nên AH = BH = AK = CK.
Xét ∆BHD (vuông tại H) và ∆CKE (vuông tại K) có:
BH = CK và (do vì ∆ABC cân tại A)
Do đó ∆HBD = ∆KCE (cạnh góc vuông – góc nhọn kề)
Suy ra BD = CE (hai cạnh tương ứng) và (hai góc tương ứng)
Nên (đối đỉnh), suy ra ∆ODE cân tại O.
Vậy A, B, D là các khẳng định đúng. Ta chọn phương án C.