Cho AB và CD là hai đường kính của đường tròn (O) vuông góc nhau. Lấy điểm E thuộc cung nhỏ BC (E khác B, C). Tia CE cắt AB tại K. Gọi I là giao điểm của ED và AB. a) Chứng minh EA là phân gi
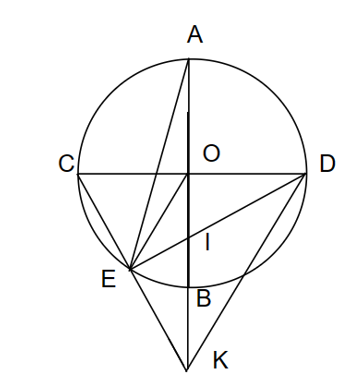
Cho AB và CD là hai đường kính của đường tròn (O) vuông góc nhau. Lấy điểm E thuộc cung nhỏ BC (E khác B, C). Tia CE cắt AB tại K. Gọi I là giao điểm của ED và AB.
a) Chứng minh EA là phân giác của góc CED.