Cho a, b, c > 0. Chứng minh : a^3/b + b^3/c + c^3/a lớn hơn bằng ab + bc + ca
Cho a, b, c > 0. Chứng minh 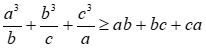 :
:
Xét hiệu : a3b−(a2+ab−b2)
=a3−a2b−ab2+b3b=(a−b)2.(a+b)b≥0(vì a,b>0)
Vậy a3b≥a2+ab−b2
Chứng minh tương tự : \frac{{{b^3}}}{c} \ge {b^2} + bc - {c^2} & & & \frac{{{c^3}}}{b} \ge {c^2} + ca - {a^2}
⇒a3b+b3c+c3a≥ab+bc+ca
Dấu xảy ra ⇔a=b=c